3D Rotational Coordinate Optimization
Update: At time of writing, this work was somewhat early stage. While it is explained briefly here, it is detailed in depth in Chapter 3 of my masters thesis.
Background
My masters advisor, Prof. Ross L. Hatton, found that choice of body coordinates impacts system stability, from a mathematical point of view. The optimal choice of coordinates, termed Minimum Perturbation Coordinates, is a particularly stable coordinate choice for robot systems.
The goal of this project (in collaboration with several other OSU robotics students) was to execute dynamic gaits (running, jumping) on Agility Robotics’ Cassie. Optimization of the robot’s rotational coordinates is necessary to effectively reconcile differences in the optimal robot trajectory and the learned motor commands. This was my role for the project.
The Project
Based on methods (and verified against) a previous conference paper, I implemented a coordinate optimizer for the 3D rotation group, SO(3). In essence, it chooses body coordinates (with respect to configuration) such that moving the robot’s actuators minimally rotates the body of the robot.
The SO(3) coordinate optimizer is highly general-purpose; it can support (in theory) robot systems with an arbitrary number of actuators, in any configuration. The objective function is defined over an N-dimensional hypercube mesh, and integrated with quadrature integration. The optimal transform is found as a set of weights on piecewise-linear basis functions, defined over the mesh.
Current Status and Future Work
The optimizer is complete, and produces minimum-perturbation coordinates for supplied systems. As an example, note the change in displacement for a test gait on a reaction-wheel satellite, in minimum perturbation coordinates:
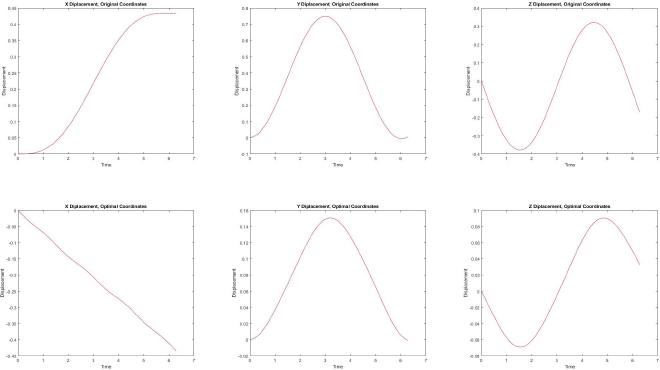
At time of writing, I’ve integrated the SO(3) coordinate optimizer into sysplotter, the Laboratory for Robotics and Applied Mechanics’ application for geometric-mechanical tools. This will allow for the study of complex systems on SO(3), with the addition of preexisting computation and visualization tools.
